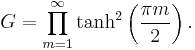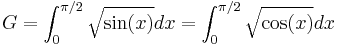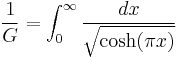Gauss's constant
In mathematics, Gauss's constant, denoted by G, is defined as the reciprocal of the arithmetic-geometric mean of 1 and the square root of 2:
The constant is named after Carl Friedrich Gauss, who on May 30, 1799 discovered that
so that
where β denotes the beta function.
Gauss' constant should not be confused with the Gaussian gravitational constant.
Contents |
Relations to other constants
Gauss's constant may be used to express the Gamma function at argument 1/4:
and since π and Γ(1/4) are algebraically independent with Γ(1/4) irrational, Gauss's constant is transcendental.
Lemniscate constants
Gauss's constant may be used in the definition of the lemniscate constants, the first of which is:
and the second constant:
which arise in finding the arc length of a lemniscate.
Other formulas
A formula for G in terms of Jacobi theta functions is given by
as well as the rapidly converging series
The constant is also given by the infinite product
It appears in the evaluation of the integrals
Gauss's constant has continued fraction [0, 1, 5, 21, 3, 4, 14, ...].
See also
References
- Weisstein, Eric W., "Gauss's Constant" from MathWorld.
- Sequences A014549 and A053002 in OEIS
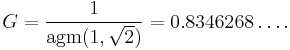
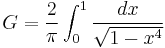
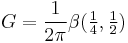
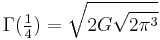
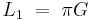
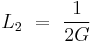
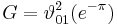
![G = \sqrt[4]{32}e^{-\frac{\pi}{3}}\left (\sum_{n = -\infty}^\infty (-1)^n e^{-2n\pi(3n%2B1)} \right )^2.](/2012-wikipedia_en_all_nopic_01_2012/I/27419a21a80e4195370dba4bdf770850.png)